
(L(N) = L(D)).īy allowing each state in the DFA D to represent a set of states in the NFA N, we are able to prove through induction that D is equivalent to N. There exists a DFA D= (Σ, Q’, q’ 0, F’, δ’) that also accepts L. Let language L ⊆ Σ*, and suppose L is accepted by NFA N = (Σ, Q, q 0, F, δ). After the jump I will prove this equivalence and also step through a short example of converting an NFA to an equivalent DFA.īefore continuing, let’s formally state the theorem we are proving: Theorem
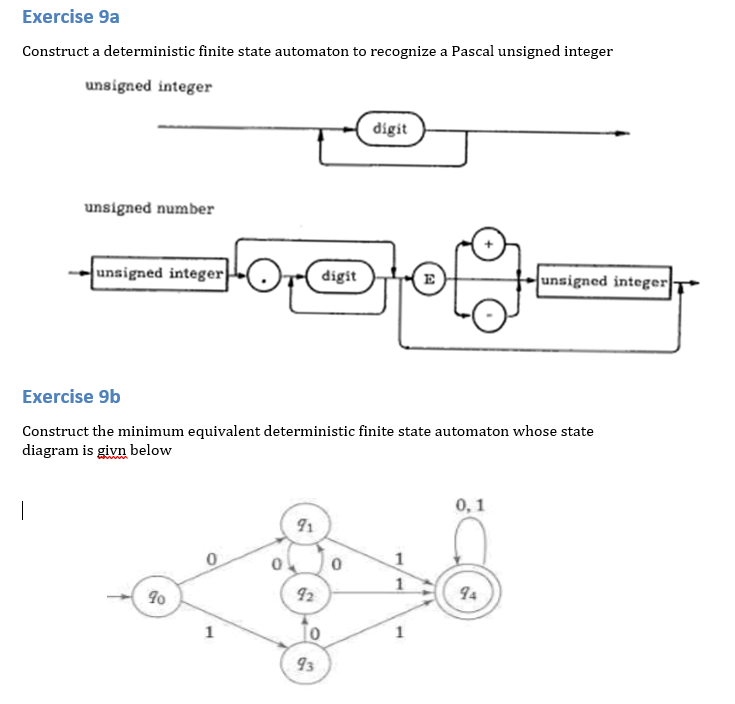
The algorithm to make the conversion from NFA to DFA is relatively simple, even if the resulting DFA is considerably more complex than the original NFA. Finite automata have two states, Accept state or Reject state. At the time of transition, the automata can either move to the next state or stay in the same state. When the desired symbol is found, then the transition occurs. It takes the string of symbol as input and changes its state accordingly. For any language recognized by an NFA, there exists a DFA that recognizes that language and vice versa. Finite automata are used to recognize patterns. It turns out, however, that they are equivalent. Superficially it would appear that deterministic and non-deterministic finite state automata are entirely separate beasts. Additionally, states in an NFA may have states that don’t require an input symbol at all, transitioning on the empty string ε. Unlike in DFA, it is possible for states in an NFA to have more than one transition per input symbol. Given this definition it isn’t too hard to figure out what an NFA is. For a given string, the path through a DFA is deterministic since there is no place along the way where the machine would have to choose between more than one transition. In automata theory DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum. In other words, whatever state the FSA is in, if it encounters a symbol for which a transition exists, there will be just one transition and obviously as a result, one follow up state. A deterministic finite state automaton has exactly one transition from every state for each possible input.
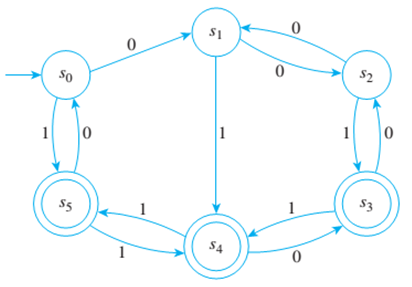
Step 5 − Then, replace all the equivalent states in one equivalence class by representative states.Finite state automata (FSA), also known as finite state machines (FSM), are usually classified as being deterministic (DFA) or non-deterministic (NFA). Step 4 − Construct Sn for n=1,2,3,….until Sn=Sn+1 Step 3 − Repeat step 2 for every Qi k in Sk and obtain all the elements of S k+1 Thus, Qi k is further divided into (k+1) equivalence classes Then, it is said that q1 and q2 are (k+1) equivalent. Find out whether δ(q1,a) and δ(q2,a) are residing in the same equivalence class δ0. If q1 and q2 are in Qik, they are (k+1) equivalent provided δ(q1,a) and δ(q2,a) are K equivalent. ducing a given deterministic finite state automaton (DFA) into a hyper- minimized DFA, which may have fewer states than the classically min- imized DFA. Generate Boolean functions for each external outputs using external inputs and present state bits Use Boolean algebra, Karnaugh maps, etc. K states: S =, where Q01 is the set of all final states and Q02 = Q-Q01 where Q is a set of all states in DFA. CHAPTER VIII FINITE STATE MACHINES (FSM) FINITE STATE MACHINES The procedure for developing a logic circuit from a state table is the same as with a regular truth table.The next state function is a combinational logic function that given the inputs and the current state, determines the next state of the systemĪ Finite State Machine consists of the following − If there are n bits of storage, there are 2n possible states. The set of states correspond to all the possible combinations of the internal storage.
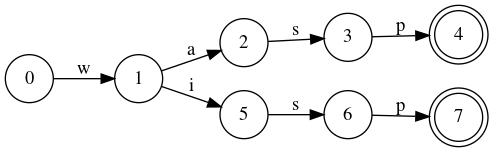
A finite state machine (FSM) which has a set of states and two functions called the next-state and output function.


 0 kommentar(er)
0 kommentar(er)
